Momchil Terziev

Momchil Terziev

Lecturer

CFD grid set-up calculator

On this page:

I am developing a web-based version of the app. At present, the web-based version of the app uses the ITTC correlation line only. I am adding further functionality. The standalone version of the webpage calculator is available here or by expanding the section below.

Web-based $y^+$ calculator

Automated definition of setttings in Star-CCM+

I created a macro that allows the entire process described in the page to take place within Star-CCM+. This can be accessed by downloading this file and opening it as a macro in Star-CCM+. The macro creates properties under parameters that can be adjusted and set as the settings in the meshing pipeline.

Background

The app uses the method for setting a grid described in my full-scale review paper. The approach uses the fact that the frictional resistance coefficient ($C_f$) may be expressed by using the Reynolds number ($Re$). Here we do not make a distinction between the local frictional resistance coefficient $C_f$ and the integral frictional resistance coefficient $C_F$.

Frictional resistance coefficient estimation methods

The following methods can be used at present:

IdentifierEquation
ITTC\(C_f=0.075/(log_{10}(Re)-2)^{2}\)
Prandtl\(C_f=0.074Re^{-1/5}\)
Telfer\(C_f=0.34Re^{-1/3}+0.0012\)
Landweber\(C_f=0.0816/(log_{10}(Re)-1.703)^2\)
Hughes\(C_f=0.067/(log_{10}(Re)-1.703)^2\)
Gadd\(C_f=0.0113/(log_{10}(Re)-3.7)^{1.15}\)
Granville\(C_f=0.0776/(log_{10}(Re)-1.88)^2+60/Re\)
Schoenherr\(0.242/\sqrt{C_f}=log_{10}(Re{\times}C_f)\)

Calculation

Once the line to calculate $C_f$ is chosen, the shear stress is predicted as:

\[\tau_w=C_f\rho U^2/2\]

Then, the first layer thickness is calculated using the desired $y^+$ through:

\[dy=y^+\nu/\sqrt{\tau_w/\rho}\]

where $\nu=\mu/\rho$ is the kinematic viscosity. We must now distribute layers over a user-specified distance, which can be specified in three ways:

  1. As a fraction of the boundary layer thickness $\delta_x=x0.382L/Re^{1/5}$ where $L$ is the ship/body length, and $x%$ is the % of the boundary layer we wish to distribute layers over.
  2. As a fraction of the ship/body length $\delta_x=x{\times}L$, where $x$ is a % of the ship/body length
  3. As a total distance $\delta_x=x$, where $x$ is a distance in m.

There is no point on distrubuting layers of constant thickness equal to \(dy\) over the entire selected distance because this would result in using unnecessarily many layers. Instead, it is possible (within Star-CCM+) to express the layer distribution as the geometric progression:

\[\delta_x=\underbrace{2dy+S{\times}2dy+S^2{\times}2dy+S^3{\times}2dy+...S^{n-1}{\times}2dy}_\text{n layers}\]

whose common ratio is $S$, a user-defined value between $1$ and $\infty$. The sum of all terms $\sum_{0}^{n-1} 2dyS^n$ is the thickness over which we wish to distribute cells. The number of cells we need is then

\[n=log[-\delta(1-S)/(2dy)+1]/log(S)\]

Note that we use \(2dy\) instead of \(dy\) because the cell centre must be located at a distance of $dy$ from the wall.

The only drawback is that we need an integer number of layers and rounding up/down may cause some disagreement between the target $y^+$ and the desired $y^+$. In general, this discrepency can be expected to be in the region of up to 20% for low $y^+$ meshes and about $\pm$10% for high $y^+$ meshes.

Free surface mesh recomendations

This recommendation applies to surface-piercing bodies moving in calm water at (depth) Froude numbers < 1. At present, the calculator only provides recommendations for the horizontal plane ($x-y$). In general, an aspect ratio of about 8 should be sufficient for the vertical dimension. The recommendations are based on the computed transverse wavelength. I will eventually include capability to predict the wavelengths of divergent waves as well.

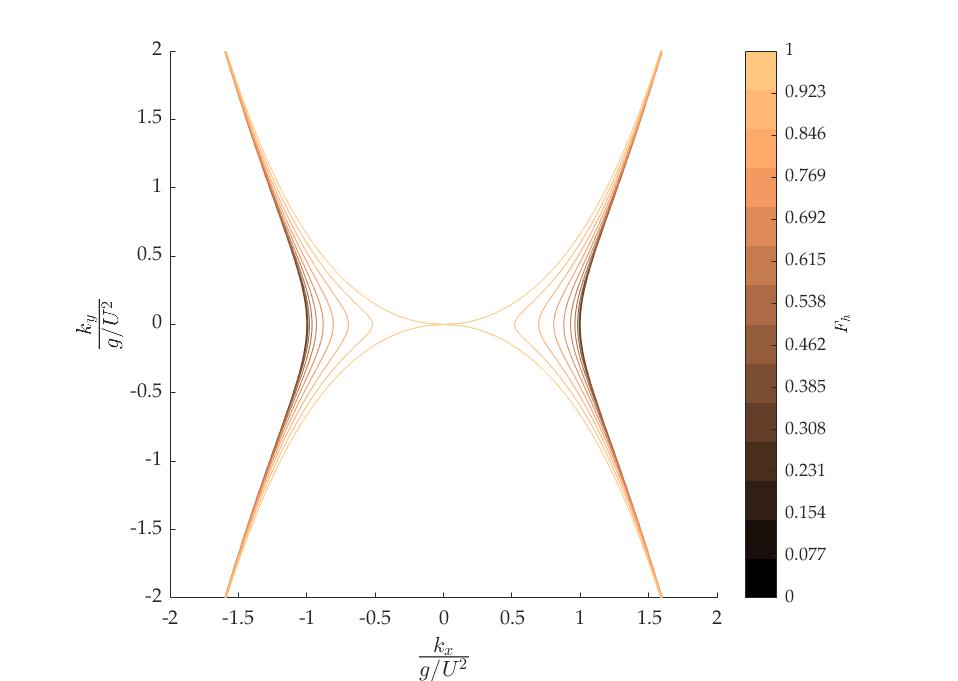
The length of a transverse wave is predicted through the Doppler shifted dispersion relation

\[\omega' = \pm\sqrt{gk\tanh{kh}}-Uk_x\]

Solving for $\omega’=0$ and $k=\sqrt{k_x^2+k_y^2}$ gives

\[U^2k^2_x-g\sqrt{k_x^2+k_y^2}\tanh{h\sqrt{k_x^2+k_y^2}}=0\]

with $h$ being the water depth. When \(kh>>1\), the results reduce to the deep water relations. To predict the wavelength, the value of $k_x$ at $k_y=0$ is computed by

\[U^2k_{c,x}^2-gk_{c,x}\tanh{hk_{c,x}}=0\]

where $k_{c,x}$ is the cut-off wavenumber. The transverse wavelength is then $\lambda=2\pi/k_{c,x}$. The number of cells we wish to distribute per wavelength are specified in the Methods section through the property Cells/$\lambda$. Shallow water effects are accounted for only when the relevant tickbox is checked. It should be kept in mind that shallow water effects can have a singnificant effect on the $y^+$ values and may cause larger deviations than expected. An example of such deviations are reported in my upcoming paper on roughness effects on ship performance in confined waters.

Click here to see the full wavenumber plane for varying depth Froude numbers $F_h$

User interface

Click here to view the app user interface.

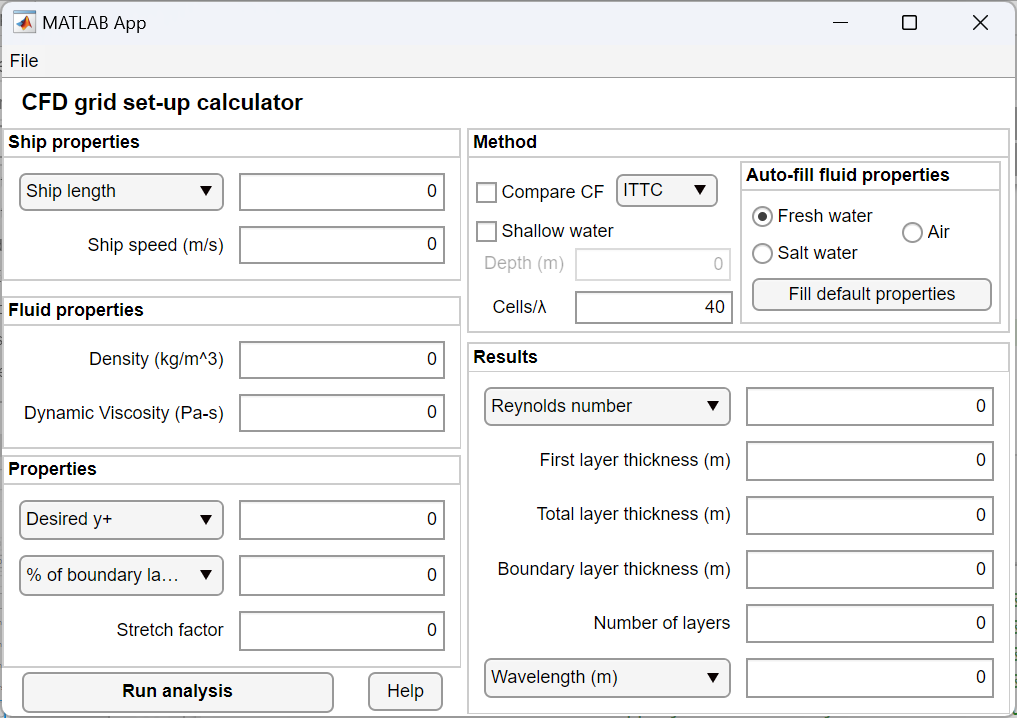
Controls

Properties according to the ITTC:

PropertyFresh waterSalt waterAirUnits
Density997.5611026.0211.18415\(kg/m^3\)
Dynamic viscosity0.000888710.001221.85508E-5\(Pa-s\)

Changing the water temperature

The temperature may be set at any value between 0.1 °C and 50 °C at 0.1 °C increments to determine the density and viscosity of the fresh water or salt water. The menu can be accessed by right-clicking anywhere in the ‘Auto-fill fluid properties’ section. Full details can be found on the ITTC webpage.

Recording outputs

The ‘File’ menu can be used to trigger continous recording of all data shown in the command window. When prompted to create a file for recording the outputs, use .txt, .rtf or any other editor extension. The same menu can be used to switch logging off, or using the Exit option under the ‘File’ menu. Closing the app otherwise will not disable logging. Use diary off to disable logging manually.

Visualising layer distribution

The placement of cell centers and vertices in terms of their y+ allocation may be viewed by right-clicking the Run button. All fields in the inputs sections must be filled prior to triggering this setting.

Download and install

The app may be downloaded here, and installed by navigating to the MATLAB Apps ribbon.

It is possible to choose the desired \(y^+\) or the number of layers if known in advance. In the latter case, the \(y^+\) is computed in place of the number of layers. These settings may be changed through the dropdown menus in the Grid properties section. Similarly, when the first layer thickness is specified, the output field displaying the first layer thickness shows the achieved \(y^+\) instead.

Wishlist and planned updates

Known problems

Last update: November 9th 2022